| Menú Matemáticas Básicas | Menú Ejercicios con Conjuntos | Tema Anterior | Tema Siguiente |
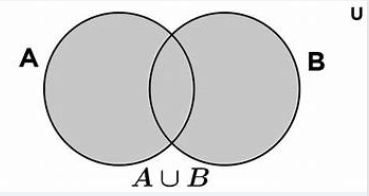
Dados dos conjuntos A y B, la UNIÓN de A y B que se denota por A ∪ B, como el conjunto
de los elementos que están en A o están en B. Aquí el o es inclusivo, es decir, incluye elementos que también pueden estar a la vez en A y en B.
El símbolo lógico ∨ se utiliza para el o cuando se describe por comprensión.
|
Tenemos el conjunto universal de las edades de los trabajadores de la empresa Cespro:
U = {18,19,21,25,28,35,42,45,56,58}
Es importante que no hayan edades iguales entre trabajadores, o sino no se podría modelar el problema mediante conjuntos.
Sea el conjunto A de los trabajadores menores de 30 años:
A = {18,19,21,25,28}
Sea B el conjunto de las edades de los trabajadores de más de 40 años:
B = {42,45,56,58}
Ahora la unión es:
A ∪ B = {18,19,21,25,28,42,45,56,58}
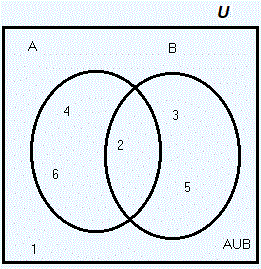
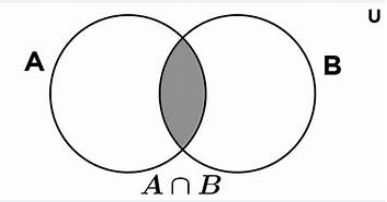
Dados dos conjuntos A y B, la INTERSECCIóN de A y B que se denota por A ∩ B, como el conjunto
de los elementos que están en A y están en B.
|
Tenemos el conjunto universal de las edades de los trabajadores de la empresa Cespro:
U = {18,19,21,25,28,35,42,45,56,58}
Es importante que no hayan edades iguales entre trabajadores, o sino no se podría modelar el problema mediante conjuntos.
Sea el conjunto A de los trabajadores menores de 40 años:
A = {18,19,21,25,28,35}
Sea B el conjunto de las edades de los trabajadores de más de 30 años:
B = {35,42,45,56,58}
Ahora la intersección es:
A ∩ B = {35}
D = A ∩ B = {2}
| Conjunto vacío Se llama conjunto vacío, y se designa por un ∅, a un conjunto que no tiene elementos.Es diferente al conjunto {∅} en el cual sí hay un elemento correspondiente al vacío. |
Conjunto Complemento
| Dado un conjunto cualquiera A del conjunto universal
U, se llama conjunto complemento de A a un conjunto Ac que tiene todos los demás elementos en U que no
están en A
Los conjuntos A y Ac (también se simboliza con A′, ∼A, o Ā ), para el conjunto complemento , contrario o negación de A. 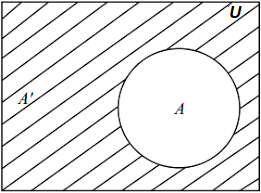
|
Diferencia
Dados dos conjuntos A y B se define la diferencia entre A y B como A − B = {x ∣ x ∈ A, y, x ∉ B}, en otras palabras, son los elementos que están en A y no están en B. 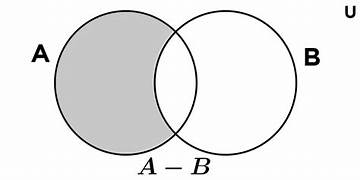 |
|
Dados dos conjuntos A y B se defince la diferencia simétrica entre A y B como A ∆ B = (A − B) ∪ (B − A) = (A ∪ B) − (A &cap: B) = {x ∣ x ∈ A, y, x ∉ B, o, x ∈ B, y, x ∉ A }, en otras palabras, son los elementos que están en A o están en B pero no en ambos a la vez. La diferencia semetrica también se asocia con el o exclusivo. |
|
Resumen de las operaciones entre conjuntos |
Sean los conjuntos:
U = {x ∈ ℕ ∣ 1 ≤ x ≤17}
S = {x ∈ U ∣ x es un número menor que 8}
W = {x ∈ U ∣ x es un número impar}
Y = {x ∈ U ∣ x es un número primo}
Z = {x ∣ 6 ≤ x ≤ 13}
Primero veamos por extensión los diferentes conjuntos:
U = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17}
S = {1,2,3,4,5,6,7}
W = {1,3,5,7,9,11,13,15,17}
Y = {2,3,5,7,11,13,17}
Z = {6,7,8,9,10,11,12,13}
Algunas operaciones entre estos:
Sc = {8,9,10,11,12,13,14,15,16,17}
S ∪ W = {1,2,3,4,5,6,7,9,11,13,17}
S ∩ W = {1,3,5,7}
W ∩ Y = {3,5,7,11,13,17}
W − Y = {1,9,15}
W ∆ Y = {1,2,9,15}
Z ∆ Y = {2,3,5,6,8,9,10,12,17}
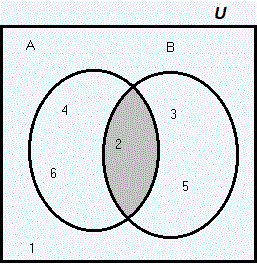
Para dos conjuntos A y B, se tienen las diferentes zonas como se describe en la siguiente imagen:
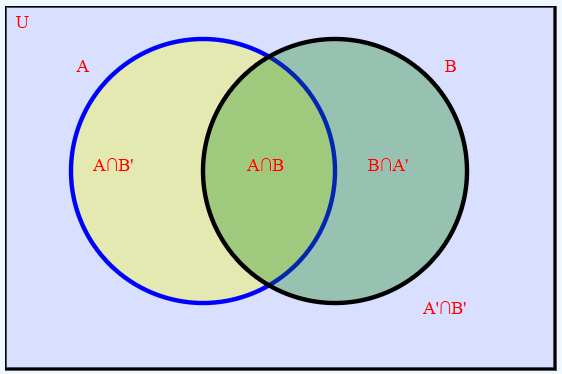
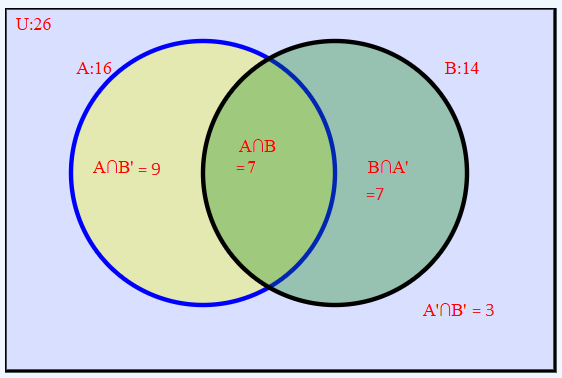
De los 26 estudiantes de un grupo, se observa si perdieron álgebra (A), o biología (B), es decir:
A: Subconjunto de estudiantes que perdieron álgebra
B: subconjunto de estudiantes que perdieron biologia
Se encuentra que:
- 16 estudiantes perdieron álgebra.
- 14 estudiantes perdieron biología
- 7 estudiantes perdieron ambas, álgebra y biología.
Con esta información se puede encontrar la demás información en las otrás zonas del diagramas de Venn. Se debe tener en cuenta que n(A) = 16 y los que perdieron únicamente álgebra correspondiente a A − B = A ∩ B' = 16 − 7 = 9. La forma A ∩ B' se puede interpretar como los que están en A Y No están en B, o en este caso los que pierden álgebra Y no pierden biología.
Una forma de encontrar A ∪ B es con:
A ∪ B = A + B − A ∩ B, que para el ejemplo tomando las
cantidades de cada conjunto o n(A) y n(B), se tiene:
n(A ∪ B) = n(A) + n(B) − n(A) ∩ n(B) = 16 + 14 − 7 = 23
Con la unión, es decir, el total que perdieron álgebra y biología, se puede hallar los que no perdieron ninguna de las
dos asignaturas, es decir:
n(A') ∩ n(B') restando del total:
n(A') ∩ n(B') = n(U) − n(A'∪ B') = 26 − 23 = 3
La solución del ejercicio es:
La Ley distributiva para números reales es
a(b + c) = ab + ac
Dos leyes distributivas similares para conjuntos y por consiguiente para operaciones con eventos, son las siguientes:
A ∩ ( B∪ C) = (A ∩ B) ∪ ( A ∩ C) A ∪ ( B∩ C) = (A ∪ B) ∩ ( A ∪ C) |
Estas leyes son útiles para tratar eventos compuestos que incluyan los conectores lógicos Y (∧) y O (∨). Estas leyes nos dicen que
A y (B o C) es equivalente a (A y B) o (A y C)
y que
A o (B y C) es equivalente a (A o B) y (A o C)
Ejemplo. Una compañía de servicios financieros está estudiando un grupo de individuos que son clientes potenciales. La compañía ofrece vender acciones, bonos y seguros de vida a sus clientes. Los eventos de interés son los siguientes:
A: el individuo posee acciones
B: el individuo posee bonos
C: el individuo tiene cobertura de seguro de vida.
Las leyes distributivas nos dicen que
A ∩ ( B∪ C) = (A ∩ B) ∪ ( A ∩ C)
A ∪ ( B∩ C) = (A ∪ B) ∩ ( A ∪ C)
La primera identidad establece que:
(Poseer Acciones) y (poseer bonos o estar asegurado) es equivalente a (poseer acciones y poseer bonos) o (poseer acciones y estar asegurado)
Ejercicio. Interprete la segunda identidad.
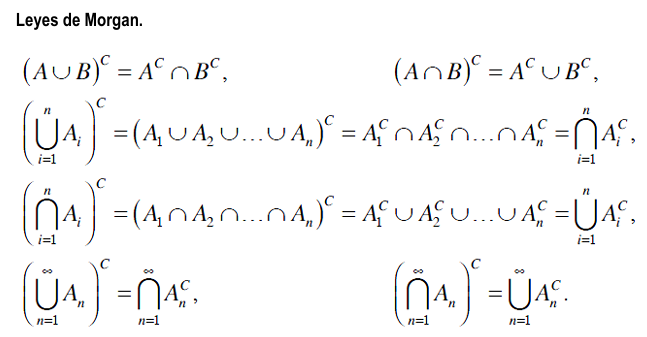 |
Dos relaciones muy útiles, son las siguientes:
i) ( A∪ B)c = Ac ∩ Bc ii) ( A∩ B)c = Ac ∪ Bc |
Una forma equivalente y alternativa de las Leyes de Morgan con la negación de un evento A como ∼ A, son:
i) ∼( A∪ B) = ∼ A ∩ ∼ B ii) ∼( A∩ B) = ∼A ∪ ∼B |
Que establecen que
no(A o B) es equivalente a (no A) y (no B)
y que
no(A y B) es equivalente a (no A) o (no B)
Ejemplo. Con los eventos A (poseer acciones) y B (poseer bonos) del ejemplo anterior. Las leyes de De Morgan establecen que
i) ∼( A∪ B) = ∼ A ∩ ∼ B, y
ii) ∼( A∩ B) = ∼A ∪ ∼B
que en palabras se interpreta la primera identidad como:
no(poseer acciones o poseer bonos) es equivalente a (no poseer acciones) y (no poseer bonos)
Ejercicio. Interprete en palabras la segunda identidad.
Ejercicios de práctica: Ejercicios con conjuntos
| Menú Matemáticas Básicas | Menú Ejercicios con Conjuntos | Tema Anterior | Tema Siguiente |