| Menú Matemáticas básicas | Menú de juegos de Matemáticas | Tema Siguiente |
El enfoque axiomático de la probabilidad se desarrolla utilizando los fundamentos de la Teoría de Conjuntos. Si está familiarizado con la notación de conjuntos, diagramas de Venn y las operaciones básicas de conjuntos (uniones, intersecciones y complementos), entonces tiene un buen comienzo con lo necesario de la teoría de conjuntos. Conjunto es el término más básico en matemáticas. Algunos sinónimos de un conjunto son clase o Colección. En esta parte presentamos el concepto de un conjunto y varias de sus operaciones y luego estudiaremos las propiedades de estas operaciones.
A lo largo de este curso, suponemos que el lector está familiarizado con los siguientes sistemas numéricos:
⋄ El conjunto de los números enteros positivos
ℕ = {1, 2, 3, ...}
⋄ El conjunto de los números enteros
ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
⋄ El conjunto de los números Racionales
ℚ = {p/q: p, q ∈ ℤ, con q ≠ 0}
⋄ El conjunto de los números Reales: ℝ
Un conjunto A es una colección de objetos bien definidos, llamados elementos del conjunto A, tal que para cualquier objeto x se cumple:
⋄ x pertenece a A, y se escribe x ∈ A.
⋄ x no pertenece a A, y se escribe x ∉ A.
El conjunto de los resultados posibles al lanzar un dado son los números 1, 2, 3, 4, 5 y 6. Estos objetos se llaman elementos o miembros del conjunto que se ha definido. Si el conjunto es lo suficientemente pequeño como para que podamos enumerar fácilmente todos sus elementos, podemos describir el conjunto al enumerar todos sus elementos entre llaves. Para el conjunto anterior, A = {1,2,3,4,5,6}. Para conjuntos grandes o infinitos, se puede utilizar la notación de conjuntos. Por ejemplo, el conjunto de todos los números reales positivos puede escribirse como:
S = {x|x es un número real y x > 0}
Normalmente se supone que los números son reales, por lo cual el conjunto anterior se escribe como
S: {x|x > 0}.
En la teoría de conjuntos, la cantidad de elementos en un conjunto tiene un nombre especial: la cardinalidad del conjunto. Escribimos n(A) para denotar la cardinalidad de el conjunto A. Si A tiene una cardinalidad finita decimos que A es un conjunto finito. De otra manera, se llama infinito. Para conjuntos infinitos, se escribe n(A) = ∞. Por ejemplo, n(ℝ) = ∞.
Ejercicio: ¿Cuál es la Cardinalidad de los siguientes conjuntos?
a) ∅
b) { ∅ }
c) {a, {a}, {a, {a}}}.
El uso importante de la teoría de conjuntos aquí es proporcionar un lenguaje preciso para tratar los resultados en un experimento de probabilidad (o experimento aleatorio).
Para comparar Números, se utulizan las desigualdades, así: decimos que 5 > 3 para indicar que Cinco es mayor que tres, o -3 > -5 para indicar la correspondiente comparación en cantidades negativas. En el caso de los conjuntos, se utilizan el concepto de subconjunto:
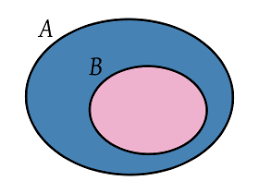
| Definición 5.1. Dados dos conjuntos A y B, se dice que B es un subconjunto de A, y se escribe B ⊆ A si y solo si cada elemento de B también es un elemento de A. Si existe un elemento de B que no es elemento de A, entonces se dice que B ⊈ A.
|
Para cualquier conjunto A, se tiene que ∅ ⊆ A ⊆ A. Esto quiere decir que cada conjunto tiene al menos dos subcojuntos, el conjunto vacío (que es en general un subconjunto de cualquier conjunto), y el mismo conjunto.
Ejemplo. Sean los conjuntos A = {2, 4, 6}, B = {2, 6}, y C = {4, 6}. Determine cuáles de estos conjuntos son subconjuntos de otros de estos conjuntos
Solución: B ⊆ A, y C ⊆ A.
Ejercicio. Dados tres conjuntos A, B y C, represente con un digrama de Venn A ⊆ B ⊆ C

Ejercicio. Dé el orden de los conjuntos numéricos : ℝ, ℕ, ℚ, ℤ usando ⊂
Ejercicio. Dé el orden de los conjuntos numéricos : ℝ, ℕ, ℚ, ℤ usando Diagrama de Venn.

Ahora, la colección de todos los subconjuntos de un conjunto A, es de gran importancia.
| Definición 5.2. El conjunto potencia de un conjunto A es otro conjunto formado por todos los subconjuntos del conjunto A. Este conjunto se representa por P(A) y tiene 2n(A) elementos. |
Ejemplo. Sea A ={1,2,3}, describa el conjunto potencia de A. Solución: ya que A tiene tres elementos, n(A) = 3, el conjunto potencia de A o P(A) es un conjunto con 23 = 8 elementos, y es:
P(A) = {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}Ejercicio. Encuentre el conjunto Potencia de A = {a, b, c}.
| Menú Matemáticas básicas | Tema Siguiente |