| Menú Probabilidad y Estadística | - | Tema Siguiente |
Hay dos escuelas de estadística: la bayesiana y la frecuentista. Sus enfoques se basan en diferentes interpretaciones del significado de probabilidad.
Los frecuentistas dicen que la probabilidad mide la frecuencia de varios resultados de un experimento. Por ejemplo, decir que al lanzar una moneda se tiene el 50% de probabilidad de que salga cara, significa que si la arrojamos muchas veces, esperamos que aproximadamente la mitad de los lanzamientos salga cara.
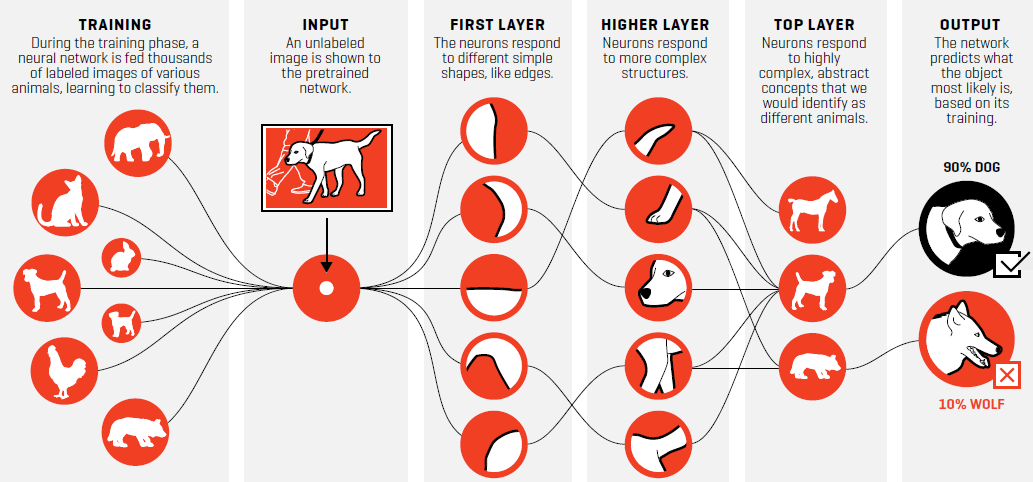
Los bayesianos dicen que la probabilidad es un concepto abstracto que mide un estado de conocimiento o un grado de creencia en una proposición determinada. En la práctica, los bayesianos no asignan un valor único a la probabilidad de que al lanzar una moneda salga cara. Más bien, consideran un rango de valores, así en la imagen 1, se observa un modelo de Deep Learning en que inicialmente se entrena el modelo computacional con miles de imágenes de animales (parte izquierda), luego al ingresar al sistema la imagen de un perro, las redes neuronales en diferentes capas comienzan a discriminar el tipo o categoría de animal, dando como resultado final de que sea un perro con uma probabilidad de un 90% y de que sea un lobo con un 10%.

Fig.1 Deep Learning para reconocimiento de imágenes. Fuente: https://fortune.com/longform/ai-artificial-intelligence-deep-machine-learning/
El enfoque frecuentista ha dominado durante mucho tiempo campos como la biología, la medicina, la salud pública y las ciencias sociales. El enfoque bayesiano ha experimentado un resurgimiento en la era de las computadoras potentes y el big data. Es especialmente útil cuando se incorporan nuevos datos en un modelo estadístico existente, por ejemplo, al entrenar un sistema de reconocimiento de imágenes o de audio.
Hoy en día, los estadísticos están creando herramientas poderosas utilizando ambos enfoques de manera complementaria.
La probabilidad y la estadística se utilizan ampliamente en las ciencias, la ingeniería, la medicina, las ciencias sociales y humanas, la economía y la informática. La lista de aplicaciones es esencialmente interminable: pruebas de un tratamiento médico contra otro (o un placebo), medidas de vinculación genética, la búsqueda de partículas elementales, aprendizaje automático para la visión o el habla, probabilidades y estrategias en juegos, modelos climáticos, previsión económica, epidemiología, marketing, modelos de riesgos (financieros, de falla, de salud o de vida). Nos basaremos en ejemplos de muchos de estos campos durante este curso.
Los científicos buscan responder preguntas utilizando métodos rigurosos y observaciones cuidadosas. Estas observaciones, recopiladas a partir de notas de campo, encuestas y experimentos, forman la columna vertebral de una investigación estadística y se denominan datos. La estadística es el estudio de la mejor manera de recopilar, analizar y sacar conclusiones de los datos.
El avance tecnológico en la informática ha contribuido enormemente al desarrollo de la estadística, sobre todo en la manipulación de la información, pues existen paquetes estadísticos de excelente calidad, como el SAS, SPSS, SCA, STATGRAPHICS, MATLAB, R, PYTHON, algunos de estos se pueden ejecutar en un ordenador o inclusive en “la nube” sin mayores exigencias tecnológicas, permitiendo el manejo de grandes volúmenes de información.
Nos ocuparemos de responder la cuestión de cómo podemos aprender sobre las poblaciones y las distribuciones de probabilidad a partir de los datos. En cualquier ciencia empírica se encontrará con el problema del razonamiento inductivo, lo que significa sacar conclusiones generales de unos pocos (o incluso muchos) casos especiales observados.
En las encuestas políticas ("¿por quién votaría en las próximas elecciones presidenciales?"), una empresa típicamente encuesta a unos pocos miles de entre millones de votantes potenciales. En los ensayos médicos, tratamos de sacar conclusiones sobre la eficacia de un fármaco o de una vacuna para toda una población a partir de solo unas pocas docenas de participantes del estudio.
Si solo observamos un subconjunto de individuos (por ejemplo, una muestra aleatoria de votantes en una encuesta de una población de interés (por ejemplo, todos los votantes que acudieron a las elecciones presidenciales), habrá cierta incertidumbre sobre si esta muestra era realmente representativa. para toda la población con respecto a la pregunta que buscamos (por ejemplo, el porcentaje de votos para un candidato en particular). Formalizar esto para uso práctico hace un uso intensivo de la teoría de la probabilidad.
La estadística hace inferencias sobre una población, partiendo de una muestra representativa de ella. Es a partir del proceso del diseño y toma de la muestra desde donde comienzan a definirse las bondades y confiabilidad de nuestras aseveraciones, hechas, preferentemente, con un mínimo costo y mínimo error posible.
| La estadística es un conjunto de técnicas que, partiendo de la observación de fenómenos, permiten al investigador obtener conclusiones útiles sobre ellos. |
|---|
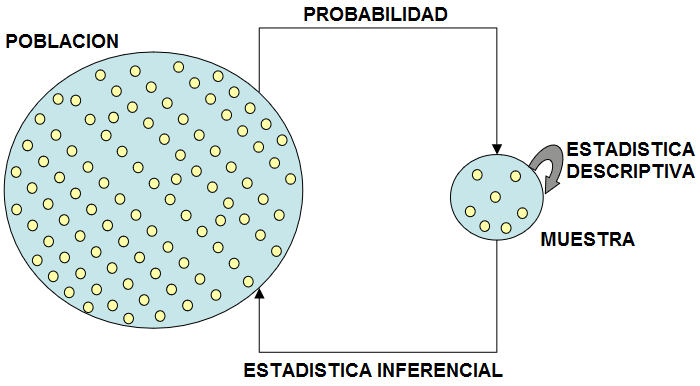 |
Imagen 2. El Dogma Central de la Estadística
El uso o la aplicación de conceptos de Probabilidad permite interpretar situaciones de la vida cotidiana a partir de los resultados de la Inferencia Estadística. Para un problema Estadístico, la muestra junto con la Estadística Inferencial, permiten obtener conclusiones acerca de alguna característica de la Población. Esto es lo que se conoce como Dogma Central de la Estadística.
En la realización de cualquier experimento cabe distinguir dos fases:
- En una primera fase de observación y análisis de sucesos, es importante recoger, ordenar y simplificar los datos.
- En una segunda fase se hace necesario interpretar los datos recogidos y extraer conclusiones a partir de estos.
En ambas fases la Estadística es una herramienta muy útil, esta es una ciencia que se ocupa de recopilar, analizar e interpretar los datos numéricos relativos a un conjunto de individuos(por ejemplo:altura de los alumnos de un colegio, casos de tuberculosis en una región determinada, espectadores de cierto programa de televisión, ...)
En la primera fase interviene la llamada Estadística Descriptiva, que proporciona un conjunto de técnicas y procedimientos para la recogida,clasificación y reducción de los datos a unas pocas medidas representativas.
En la segunda fase desempeña un papel relevante la denominada Estadística Inductiva o Inferencial, que dota al investigador de un conjunto de métodos para extraer conclusiones de los datos obtenidos.
Este primer curso da una breve introducción a la Estadística Descriptiva.
Definición 1.1. Algunos conceptos generales- Población estadística es el conjunto de elementos sobre el que recae las observaciones. Es el conjunto de todos los individuos (personas, objetos, animales, etc.) que contienen información sobre el fenómeno que se estudia. Por ejemplo, si estudiamos el precio de la vivienda en una ciudad, la población será el total de las viviendas de dicha ciudad.- Unidad estadística o individuo es cada uno de los elementos que componen una población. Es cualquier elemento que contiene información sobre el fenómeno que se estudia. Así, si estudiamos la altura de los niños de una clase, cada alumno es un individuo; si estudiamos el precio de la vivienda, cada vivienda es un individuo. - Muestra es un subconjunto de elementos de la población, a la ques sustituye cuando el estudio de todos los individuos de la misma es difícil o costoso. Así, si se estudia el precio de la vivienda de una ciudad, lo normal será no recoger información sobre todas las viviendas de la ciudad (sería una labor muy compleja), sino que se suele seleccionar un subgrupo (muestra) que se entienda que es suficientemente representativo. - Tamaño es el número de individuos de la población o muestra. Para muchos estudios es fundamental definir bien este factor por lo cual hay varios métodos para obtenerlo. - Carácter es una cualidad o propiedad observable que presenta variación de unos individuos a otros. Se clasifican en cuantitativos o cualitativos, según que pueda o no asignárseles un valor numérico. - Modalidad es cada uno de los valores de un carácter cualitativo. - Variable estadística es un sinónimo de carácter cuantitativo. Las variables estadísticas se dividen en continuas o discretas, según que puedan o no tomar todos los valores dentro de un intervalo dado. |
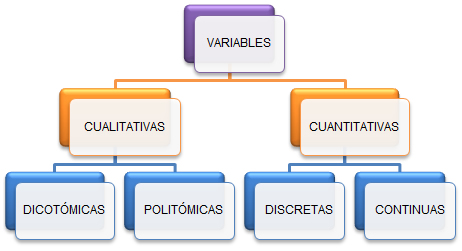 |
Las variables estadísticas se pueden clasificar de varias maneras, entre estas según su naturaleza, pueden ser de dos tipos:
| Tipos | Propiedades | Ejemplos |
|---|---|---|
| Cualitativas a atributos | Los valores que toma la variable son cualidades, no números. No se pueden medir numéricamente (por ejemplo: , sexo) |
- Deporte: fútbol, balonmano, atletismo,... - Nacionalidad: colombiano, peruano, español,... - Color de la piel. - Sexo: hombre, mujer. |
| Cuantitativas | Los valores que toma la variable son números. . |
- Número de páginas de un libro. - Edad |
A su vez, las variables cuantitativas se clasifican en:
| Tipos | Propiedades | Ejemplos |
| Discretas | En cada tramo, la variable sólo puede tomar un número determinado de valores. Se puede asociar con datos obtenidos de procesos en que se cuenta el número de casos. |
- Número de páginas de un libro: 210 o 211 pero no 210,5. - Número que se ocupa en una fila: 1, 2, 3... |
| Continuas | En cada tramo, la variable puede tomar infinitos valores. Se puede asociar con la toma de datos de una situación en que se midealguna característica. |
- Altura de una persona: entre 170 cm y 180 cm la altura puede ser 171 cm, 171.5 cm... - Peso de un recién nacido: 3502.5 g, 3600.8 g, etc. |
Las variables también se pueden clasificar en:
Variables unidimensionales: sólo recogen información sobre una característica
(por ejemplo: edad de los estudiantes de una clase).
Variables bidimensionales: recogen información sobre dos características de la
población (por ejemplo: edad y altura de los alumnos de una clase).
Variables pluridimensionales: recogen información sobre tres o más
características (por ejemplo: edad, altura y peso de los alumnos de una clase).
Dicotómicas:Es aquella que tiene solo dos categorías de presentarse es decir, que puede asumir solo dos valores posibles
Politómicas:Es aquella que tiene tres o más categorías de presentarse.
Uno de los principales problemas con los que se encuentra la Medición al tratar con variables que no se puede cuantificar de la misma forma que en las ciencias naturales y por tanto no se tiene los instrumentos necesarios para medir los aspectos de la característica a evaluar.
Las escalas de medida permiten realizar un tipo determinado de operaciones con los números. Stevens propone a partir de su definición clásica de asignar números a objetos o acontecimientos de acuerdo con reglas, cuatro escalas: nominal, ordinal, de intervalo y de razón, que posteriormente aumenta a cinco con la escala de intervalo logarítmico.
Según la Escala de Medición, las variables pueden ser Nominal y Ordinal para las Cualitativas, y para las Cuantitativas se clasifican entre De Intervalo y De Razón. Sus características son:
| Tipo | Propiedades | Ejemplos |
|---|---|---|
| Cualitativa Nominal | - Caracterizada por categorías de eventos mutuamente excluyentes y colectivamente exhaustivos. - Denotan atributos o características únicas. -Su fin es identificar sujetos/objetos dentro de una distribución, por lo que únicamente podremos establecer las relaciones de igualdad/desigualdad entre los sujetos/objetos de una distribución. |
- Nombre o marca - Estado civil - Color - Nacionalidad |
| Cualitativa Ordinal | - Se caracteriza por una relación de Orden dentro de las categorías, tal como de Menor a Mayor, de Peor a Mejor, etc., en que no hay una cuantificación exacta entre una y otra categoría, solamente se establece que hay un orden creciente o decreciente en algún sentido entre estas. - La distancia entre sus unidades no es uniforme. De esta forma, podemos decir que A está por encima que B, pero no que sea el doble o que sea la mitad uno que otro. Un ejemplo es el orden de llegada en una carrera. - Además del atributo de igualdad/desigualdad, en esta escala tambiént se establece o agrega el ordenamiento de sus componentes.
|
- Primero, Segundo, Tercero - Aguo, Crónico. - Estrato socioeconómico. - Nivel de estudios: Primaria, bachiller, técnico, tecnólogo, profesional, especialista, magíster, Doctor, Post-doctor. |
| Cuantitativa De Intervalo | - En esta escala la distancia entre las unidades de medida sí es uniforme, de forma que podemos decir que D es el doble que A, por ejemplo. Por ello, permite realizar operaciones matemáticas, como suma, resta, multiplicación o división. - El cero es arbitrario ya que no indica la ausencia del atributo o característica que se mide. Como ejemplo la escala para medir la temperatura en grados Celsius, en la que el cero es relativo.
|
- Escala de temperatura en grados Celsius. No se puede afirmar que una Temperatura de 0°C sea la ausencia de la característica a medir (la Temperatura) - Coeficiente Intelectual: Va en una escala de 0 a 204 o un poco superior. Un valor de cero indicaría ausencia absoluta de inteligencia, lo cual no es posible en un ser humano, según muchos pedagogos. |
| Cuantitativa De Razón | Similar a la de intervalo, con la única diferencia que el cero en esta escala sí indica la ausencia de atributo, es cero absoluto. - En ambas escalas 4 es doble que 2 (2+2=4), o 4 es la mitad que 8, por ejemplo, debido a que la distancia entre sus unidades de medida es uniforme. |
- Masa: en gramos, por ejemplo si se busca la presencia la mercurio en una muestra de agua, y resulta que es cero, indica que efectivamente no hay presencia del metal en esta agua. - Altura en centímetros, Si el gigante Juan mide 210 cm, y la pequeña sofía mide 105 cm, luego Juan tiene el Doble de estatura que Sofía. |
| Menú Probabilidad y Estadística | - | Tema Siguiente |